Retro Telecine

To fit the camera inside the projector lamphouse, it has to be pretty close to the film. That means a short focal length lens – the typical 50mm enlarger lens won’t work. On the other hand, the lens can’t be too close to the film, or it will run into the shutter and claw.

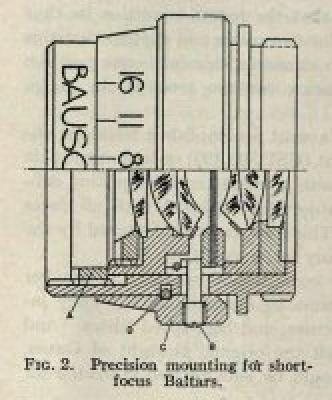I happened to have an old lens of the ideal focal length. It’s a Bausch & Lomb Baltar 17.5mm f2.3. It was a state-of-the-art 16mm movie camera lens in 1946, and it’s design is excellent for this job. It has an adjustable aperture, and as is typical, it seems to give the best results at a mid range aperture of f4 or f5.6.

The 8mm film frame has a diagonal of about 5.5mm. The CCD in the camera has a diagonal of 4.5mm. So the magnification required is about 0.8x. At magnifications this close to 1, the distance from the film plane to the CCD focal plane is roughly 4x the lens focal length, or 70mm. This makes a very compact camera unit …

… that fits nicely in the lamphouse of the projector …

The lens and camera are mounted on a brass plate that slides over two standoff posts attached to the projector lamp mounting plate. Springs over the posts press the camera plate against two thumbscrews mounted above and below the camera, in a bridge plate fixed to the ends of the posts. Turning these screws together adjusts focus. Individually, they tilt the camera plate slightly, aiming the camera and lens up or down to easily align the camera field with the film frame vertically. A third thumbscrew in a block on the back of the bridge plate moves a standoff post attached to the camera plate to tilt it from side to side and thus adjust horizontal framing.

The lens is mounted on a focusing helicoid, but at magnifications near 1, moving the lens mostly changes magnification, without changing focus very much. So I adjust the mag first, by turning the lens mount, then adjust focus and framing with the camera screws. Setup is quick and easy, and it’s much simpler and easier to construct than X/Y/Z translation mechanisms.

There are five springs altogether – the two post springs, a spring that holds the camera plate tilt post against the horizontal tilt screw, and two more that force the plate sideways against the main posts…

The springs, screws and posts perfectly constrain the position of the plate, so it cannot shift if the projector is bumped.

I captured the image below just to confirm that the lens is sharp enough to not limit the resolution of the movie captures. Lacking a micro resolution target, I used a PROM chip, 3.5mm square, which provides plenty of fine lines. It’s captured with the webcam and lens at the same magnification I need for the telecine. The blue and orange colored bands in the middle of the chip are the result of the fine pattern aliasing on the color filter array of the CCD. This is the sign that the lens resolution is more than adequate. Grainy 8mm film doesn’t have such fine line patterns, so we won’t see aliasing in movie frames.